互质数的定义及解释
作者:佚名 来源:未知 时间:2024-11-18
在数学的世界里,有许多令人着迷的概念和理论,它们或简单直观,或抽象复杂,共同构建起了这座智慧的殿堂。其中,“互质数”这一概念,虽看似不起眼,却蕴含着丰富的数学内涵和广泛的应用价值。本文将从定义解析、性质探讨、实际应用、历史渊源以及文化意义等多个维度,带领读者一窥互质数的奥秘。
定义解析:互质数的数学表述
互质数,简而言之,是指两个或多个正整数之间的一种特殊关系。如果两个正整数a和b的最大公约数(GCD)为1,即gcd(a, b) = 1,则称a和b是互质的。这里需要强调的是,互质并不要求这两个数本身为质数,而是指它们之间没有除了1以外的共同因子。例如,8和15是互质的,因为它们的最大公约数是1,尽管它们都不是质数。
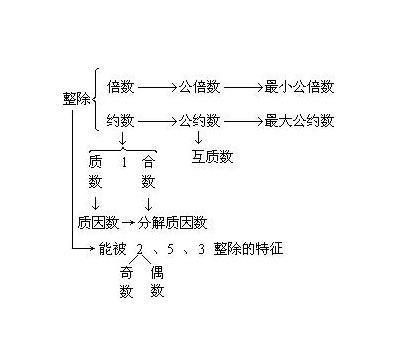
进一步地,如果一组数中的任意两个数都是互质的,那么这组数就被称为两两互质。例如,{2, 3, 5}就是一组两两互质的数,因为2、3、5之间任意两个数的最大公约数都是1。
性质探讨:互质数的数学特性
互质数具有一系列有趣的数学性质,这些性质不仅加深了我们对互质数的理解,也为解决数学问题提供了有力的工具。
1. 乘积性质:如果a和b是互质的,c是任意整数,那么ac和bc也是互质的。这一性质说明,互质关系在乘法运算下是保持不变的,这为我们证明某些数学定理提供了便利。
2. 同余性质:在模运算中,互质数扮演着重要角色。如果a和m是互质的,那么a关于模m的乘法逆元存在且唯一。这意味着,对于任意整数b,方程ax ≡ b (mod m)总有解,且解唯一确定(在模m的意义下)。这一性质在密码学、编码理论等领域有着广泛应用。
3. 质因数分解:如果a和b是互质的,那么a和b的质因数分解式中的质因数不会重叠。这一性质有助于我们快速判断两个数是否互质,因为只需检查它们的质因数是否完全相同即可。
4. 欧几里得算法:计算两个数的最大公约数是判断它们是否互质的关键步骤。欧几里得算法提供了一种高效计算最大公约数的方法,从而成为判断互质性的有力工具。
实际应用:互质数在生活中的角色
互质数不仅是一个纯粹的数学概念,它在现实生活中也有着广泛的应用,尤其是在计算机科学、密码学、统计学等领域。
1. 密码学:在公钥密码系统中,如RSA算法,互质数的性质被用来确保信息的安全性。RSA算法依赖于大数的质因数分解难题,而互质数的选择是构建安全密钥对的基础。
2. 编码理论:在数据通信中,为了确保信息的准确无误地传输,常采用编码技术。互质数在构建某些类型的编码方案时发挥着关键作用,如循环冗余校验(CRC)算法中,就利用了互质数的性质来检测数据传输中的错误。
3. 统计学:在抽样调查中,为了获得具有代表性的样本,经常需要采用系统抽样法。此时,如果样本间隔与总体容量互质,可以确保样本在总体中的均匀分布,从而提高抽样的准确性。
4. 游戏设计:在一些策略游戏或角色扮演游戏中,为了平衡游戏机制,设计师会利用互质数的性质来设计游戏规则,确保每个玩家都有公平的机会获得资源或奖励。
历史渊源:互质数的数学之旅
互质数的概念并非现代数学的产物,它的起源可以追溯到古代数学的发展初期。在古希腊,数学家们就开始研究整数的性质,包括质数、合数以及它们之间的关系。虽然互质数作为一个明确的概念可能直到更晚的时期才被明确提出,但古希腊数学家们对于整数间无公因关系的认识,无疑为互质数概念的形成奠定了基础。
进入中世纪,随着数学研究的深入,互质数的性质开始被系统地探讨和证明。欧几里得的《几何原本》中,虽然未直接提及互质数,但其关于最大公约数的论述,为互质数的研究提供了重要的理论基础。
到了近代,随着数学分支的不断细化,互质数的研究也逐渐深入到数论、代数、组合数学等多个领域。特别是随着计算机科学的兴起,互质数的应用价值得到了更广泛的认可,推动了其在现代数学和科学技术中的深入研究。
文化意义:互质数与人类智慧的结晶
互质数不仅仅是数学公式和定理的堆砌,它还承载着人类智慧的结晶,反映了人类对自然界规律的深刻洞察。从古希腊哲学家毕达哥拉斯提出的“万物皆数”的理念,到现代数学家们对互质数性质的深入挖掘,这一过程中,人类不断挑战自我,探索未知,推动了数学乃至整个科学的发展。
互质数的概念也体现了数学中的简洁美。在数学的世界里,简单而深刻的规律往往比复杂的表象更能触动人心。互质数以其简洁的定义和丰富的性质,展示了数学这门学科独特的魅力。
此外,互质数的研究还促进了跨学科的合作与交流。在密码学、计算机科学等领域,互质数的应用激发了科学家们对数学基础理论的重新审视和深入研究,推动了学科间的融合与创新。
总之,互质数作为数学中的一个基本概念,虽然看似简单,却蕴含着深刻的数学内涵和广泛的应用价值。它不仅是我们理解整数性质、解决数学问题的有力工具,也是人类智慧的结晶,展示了数学这门学科无尽的魅力和广阔的应用前景。在未来的科学探索中,互质数无疑将继续发挥其独特的作用,引领我们走向更加深邃的数学世界。
- 上一篇: 2021苹果秋季发布会直播在哪里看?
- 下一篇: 百度影音下载最新电影与电视剧教程






























