如何求解x的平方
作者:佚名 来源:未知 时间:2024-11-21
在数学的世界中,“x的平方怎么解”这一问题看似简单,实则蕴含着丰富的内涵与广泛的应用。它不仅关乎代数方程的基本求解技巧,还与几何、函数、微积分等多个数学分支紧密相连,是学习数学过程中不可或缺的一环。本文将从定义出发,逐步探讨x的平方在不同情境下的解法,并结合实例,揭示其背后的数学逻辑与美学。
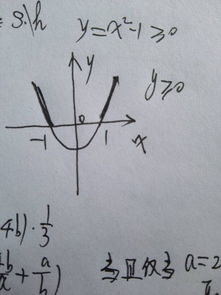
一、x的平方:基本定义与性质
首先,我们需要明确“x的平方”这一概念。在数学中,x的平方指的是x乘以自身,用数学符号表示为x²。这是一个基本的代数运算,其结果是一个关于x的二次多项式。值得注意的是,对于任意实数x,x²总是非负的(即x²≥0),这是由乘法的性质决定的。当x=0时,x²取得最小值0;而当x取正数或负数时,x²均大于0,且正数的平方与对应负数的平方相等(例如,4²=(-4)²=16),体现了平方运算的偶函数性质。
二、解方程:x²=a的形式
当我们遇到形如x²=a的方程时,首先需要判断a的正负性,因为这将直接影响方程的解的结构。

当a>0时:方程有两个不相等的实数解,分别为正根和负根,即x=√a 或 x=-√a。例如,x²=9的解为x=3或x=-3。
当a=0时:方程有一个重根,即x=0。这是因为任何实数的平方都不可能为负,所以只有当x=0时,x²才能等于0。
当a<0时:在实数范围内,方程没有解,因为任何实数的平方都是非负的。但在复数范围内,我们可以找到解,形式为x=±√(-a)i,其中i是虚数单位,满足i²=-1。例如,x²=-4的复数解为x=2i或x=-2i。
三、二次方程:ax²+bx+c=0的求解
当问题升级到一般的二次方程ax²+bx+c=0时,我们需要使用更为复杂的求解方法,即求根公式(也称为韦达定理)。求根公式为:
x = [-b ± √(b² - 4ac)] / (2a)
这里,判别式Δ=b²-4ac的值决定了方程的解的类型:
当Δ>0时:方程有两个不相等的实数解。
当Δ=0时:方程有两个相等的实数解,即一个重根。
当Δ<0时:方程在实数范围内没有解,但在复数范围内有两个解。
例如,对于方程x²-4x+4=0,我们有a=1, b=-4, c=4,所以Δ=(-4)²-4×1×4=0,根据求根公式,方程的唯一解为x=[-(-4)]/(2×1)=2,即x=2(重根)。
四、几何视角下的x²
从几何角度看,x²与抛物线紧密相关。考虑函数y=x²,这是一条开口向上的抛物线,其顶点位于原点(0,0)。抛物线y=x²的图形对称于y轴,对于任意点P(x,x²)在抛物线上,都有点P'(-x,x²)与之关于y轴对称。这种对称性反映了x²的偶函数性质。
此外,抛物线y=ax²+bx+c(a≠0)代表了一类更一般的二次函数图像,其形状、开口方向、顶点位置等由系数a, b, c共同决定。通过配方,我们可以将y=ax²+bx+c转化为顶点式y=a(x-h)²+k,从而直接读出抛物线的顶点坐标(h,k)及其开口方向(由a的符号决定)。
五、微积分中的x²
在微积分领域,x²同样扮演着重要角色。作为多项式函数,x²是可导的,其导数为2x,这反映了函数在任意点处的切线斜率。进一步,x²也是可积的,其不定积分为(1/3)x³+C,其中C是积分常数。
在优化问题中,x²常被用作目标函数或约束条件的一部分。例如,在寻找最小值问题中,函数f(x)=x²的全局最小值出现在x=0处,此时f(x)=0。这种性质使得x²成为许多优化算法中的基准函数之一。
六、应用实例:从物理到经济学
x²的应用远不止于数学本身,它在物理学、工程学、经济学等多个领域都有广泛的应用。
物理学:在经典力学中,x²经常出现在动能表达式(1/2)mv²中(其中v为速度,可视为位移x对时间的导数),以及势能函数中(如重力势能mgh,其中h可视为位移x的函数)。此外,在简谐振动中,位移x与时间t的关系也常表现为正弦或余弦函数的平方形式。
工程学:在结构分析中,梁的弯曲、应力的计算等常涉及x²的表达式,用于描述变形、应力分布等。
经济学:在成本效益分析中,x²可用于表示成本函数、收益函数或损失函数的一部分,帮助决策者评估不同策略下的经济效果。
结语
综上所述,“x的平方怎么解”这一问题,虽然看似简单,但其背后蕴含着丰富的数学原理与广泛的应用场景。从基本的代数运算到复杂的二次方程求解,从几何图形的描绘到微积分的应用,x²都以其独特的魅力,连接着数学的各个分支,也桥接了数学与现实生活之间的鸿沟。通过对x²的深入探索,我们不仅能够更好地理解数学的本质,还能发现它在解决实际问题中的巨大价值。
- 上一篇: 重庆个人档案所在地查询方法
- 下一篇: 如何在掌上道聚城轻松查看个人消费记录




































