探索斐波那契数列:自然界的奇妙密码
作者:佚名 来源:未知 时间:2024-11-21
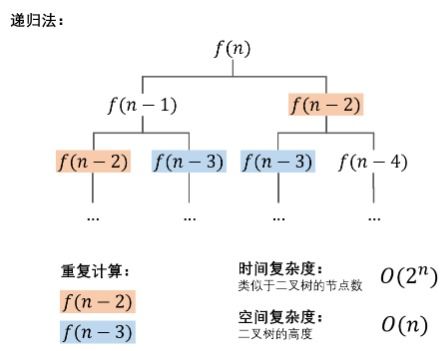
斐波那契数列,又称黄金分割数列,是一个在数学上极为经典且充满魅力的数列。它由意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci)提出,因而得名。斐波那契数列的定义简单而直观:它的前两项分别是0和1,从第三项开始,每一项都是前两项之和。即,F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)。
斐波那契数列的基本形式
斐波那契数列通常以如下形式出现:0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368……这个数列的每一项都严格遵循递归定义,从第三项开始,每一项都是前两项的和。
斐波那契数列的通项公式
斐波那契数列的通项公式较为复杂,但它在理论上可以精确地表达数列的任意一项。该公式又称为“比内公式”,是用无理数表示有理数的一个范例。通项公式为:
\[ F(n) = \frac{1}{\sqrt{5}} \left[ \left( \frac{1 + \sqrt{5}}{2} \right)^n - \left( \frac{1 - \sqrt{5}}{2} \right)^n \right] \]

这个公式的推导过程涉及线性代数中的特征方程解法,或是通过待定系数法构造等比数列来求解。无论采用哪种方法,都体现了数学中抽象思维和逻辑推理的魅力。
斐波那契数列的性质
斐波那契数列不仅具有简单的递推关系,还蕴含了许多令人着迷的性质。
1. 模除周期性:数列中的某个数模除某个数的结果会呈现一定的周期性。这源于数列的递推性质,一旦有两个连续的数的模除结果分别等于数列的前两项的模除结果,就标志着一个新的周期的开始。
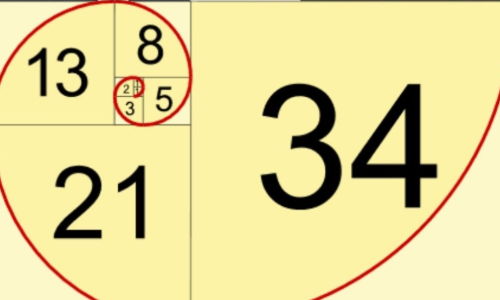
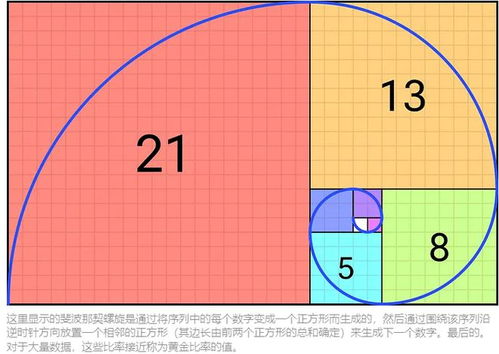
2. 黄金分割:随着项数的增加,相邻两项的比值逐渐接近黄金分割值0.618。这个性质使得斐波那契数列与黄金分割有着密不可分的联系,也进一步增加了数列的神秘色彩。
3. 平方与前后项:从第二项开始,每个奇数项的平方都比前后两项之积多一,每个偶数项的平方比前后两项之积少一。
4. 集合子集个数:斐波那契数列的第n+2项代表了集合{1, 2, ..., n}中所有不包含相邻正整数的子集的个数。
5. 隔项关系:满足f(2n-2m-2)[f(2n)+f(2n+2)]=f(2m+2)+f(4n-2m),其中n>m≥-1,且n≥1。
6. 两倍项关系:f(2n)/f(n)=f(n-1)+f(n+1)。
7. 尾数循环:斐波那契数列的个位数呈现60的周期性,最后两位呈现300的周期性,最后三位呈现1500的周期性。
斐波那契数列的现实应用
斐波那契数列不仅在数学上具有重要意义,还在众多实际领域中得到广泛应用。
1. 自然界中的形态:斐波那契数列在自然界中随处可见,如植物的叶子排列、螺旋壳的形状、花朵的排列方式等。这种数列被认为与自然界中的最佳生长和效率有关。
2. 股票市场和技术分析:在金融市场,斐波那契数列常被用于技术分析。通过将斐波那契数列应用到价格走势图表中,可以帮助识别可能的支撑位和阻力位,从而指导投资决策。
3. 编程算法:斐波那契数列是练习递归思维和算法设计的好例子。在编写递归函数时,使用斐波那契数列可以帮助学生更好地理解递归算法的原理。
4. 设计和艺术:斐波那契数列的比例和对称性被认为具有美学上的吸引力,因此在设计和艺术领域经常被采用。建筑、绘画、雕塑等艺术作品中的比例和布局常常遵循斐波那契数列。
5. 数学教育:斐波那契数列是数学教育中的重要示例,它有助于学生理解数列、递归和数学规律等概念。
6. 网络优化:在分配资源、制定时间表或调度任务时,斐波那契数列可以帮助找到最佳的排列方式,从而优化网络性能。
7. 数据分析:在时间序列分析中,斐波那契数列模型可以用于预测和趋势分析,为数据科学家提供有用的工具。
8. 计算机图形学:斐波那契数列的比例关系可以应用于计算机图形学中的几何形状生成和渲染过程,创造出具有艺术感和视觉吸引力的图像和动画效果。
9. 游戏设计:在游戏设计中,斐波那契数列的规律可以用于关卡设计、道具获取、难度递增等方面,提供更佳的游戏体验。
斐波那契数列的研究与影响
斐波那契数列的研究历史悠久,从它的提出至今已有数百年的时间。在这个过程中,数学家们不断挖掘其背后的数学原理,拓展其应用领域。美国数学会从1963年起出版了以《斐波那契数列季刊》为名的一份数学杂志,专门刊载这方面的研究成果。
斐波那契数列的影响力不仅限于数学界。在艺术领域,黄金分割比例被广泛认为是最具美感的比例之一,而斐波那契数列正是与黄金分割紧密相连的。在建筑设计中,许多经典作品都采用了斐波那契数列的比例关系,体现了数学与艺术的完美结合。
此外,斐波那契数列还激发了人们对自然界的探索。科学家们发现,许多自然现象都可以用斐波那契数列来描述,这进一步证明了数学在解释自然规律方面的重要作用。
结语
斐波那契数列是一个充满魅力的数学数列,它以其简单的递推关系和丰富的性质吸引了无数数学爱好者的目光。从数学原理到现实应用,从自然界到艺术领域,斐波那契数列都展现出了其广泛的影响力和实用价值。通过深入了解斐波那契数列,我们可以更好地领略数学的魅力,发现数学与现实生活之间的紧密联系。同时,斐波那契数列也提醒我们,数学不仅仅是一门抽象的学科,它更是人类智慧和创造力的结晶,不断推动着科学和社会的发展。
- 上一篇: 轻松区分阴历与阳历,一看就懂!
- 下一篇: 掌握“12110”短信报警技巧,紧急时刻救援无忧!





































