最小素数

在数学的世界里，有一个既简单又神秘的数字，它不仅是所有质数中的“领头羊”，更是数学基础概念的基石之一。这个数字，就是我们所称之为“最小的质数”——2。让我们一同踏上探索之旅，深入了解这个看似平凡却意义非凡的数字。

质数的定义与特性

首先，要谈及2作为最小质数的地位，我们必须明确什么是质数。质数，指的是在大于1的自然数中，除了1和它本身以外不再有其他因数的数。换句话说，一个数如果只能被1和它自己整除，那么这个数就是质数。比如2、3、5、7等都是质数，因为它们无法被除了1和自身以外的其他数整除。

质数的特性决定了它们在数学中的独特性。它们是构建自然数系统的基本元素之一，如同搭建高楼大厦的砖石。此外，质数在密码学、计算机科学等领域也有着广泛的应用，因为它们的难以预测性和分解性使其成为加密和解密算法的关键。

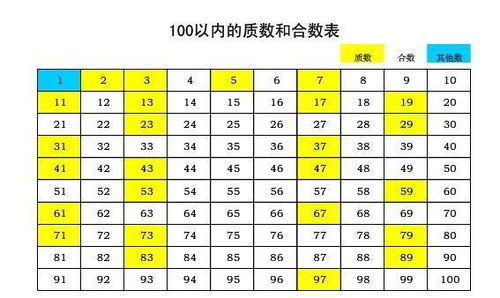
为什么2是最小的质数？

现在，让我们聚焦于我们的主角——2。为什么2是最小的质数呢？这要从质数的定义出发。根据质数的定义，一个数要被称为质数，它必须大于1，并且只有1和它本身两个因数。那么，我们逐一检查自然数：

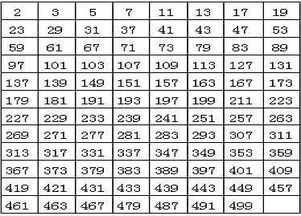
1：虽然它是自然数的一部分，但根据质数的定义，质数必须大于1，因此1被排除在质数之外。

2：2只能被1和自己（即2）整除，没有其他因数，因此它符合质数的定义。而且，它是大于1的最小自然数，所以自然而然地成为了最小的质数。

3及以上的数：虽然它们也可能符合质数的定义（比如3、5、7等），但它们都比2大，因此无法撼动2作为最小质数的地位。

综上所述，2凭借其独特的数学性质，成为了所有质数中的“老大哥”。

2在数学与现实生活中的应用

2作为最小的质数，不仅在数学理论上占据着重要位置，而且在现实生活中也有着广泛的应用。以下是一些具体的例子：

二进制系统：在计算机科学中，二进制系统是以2为基数的数制系统。它只有两个数字符号：0和1。这种系统简化了计算机的运算过程，使得计算机能够高效地处理信息。而这一切的起点，正是那个最小的质数——2。

几何学：在几何学中，2也是不可或缺的元素。比如，一个点确定一条直线，而两条不重合的直线可以确定一个平面。这里的“2”不仅代表了数量上的简单叠加，更体现了空间结构中的基本规律。

密码学：在密码学领域，质数尤其是大质数扮演着至关重要的角色。现代加密技术如RSA算法就依赖于大质数的难以分解性来保障信息的安全性。虽然2作为最小的质数在RSA算法中并不直接用于加密，但它所代表的质数概念却是整个算法的基础。

物理与化学：在物理和化学领域，2也经常出现。比如，分子中的原子通常以成对的形式存在（如氢分子H2），这是因为电子的成对排列有助于稳定分子的结构。此外，在量子力学中，自旋为1/2的粒子（如电子）也遵循着与2有关的规律。

探索2背后的数学奥秘

2不仅是一个简单的数字，它还蕴含着许多深刻的数学奥秘。以下是一些与2相关的数学概念和定理：

哥德巴赫猜想：这是一个著名的数学猜想，它提出任何大于2的偶数都可以表示为两个质数之和。虽然这个猜想至今仍未被证明或反驳，但它激发了无数数学家对质数和偶数性质的深入探索。在这个过程中，2作为最小的质数，自然而然地成为了研究的起点。

费马小定理：这是一个关于质数的定理，它指出如果p是一个质数，且a是一个整数（a不被p整除），那么a^(p-1)除以p的余数总是1。这个定理在数论和密码学中有着广泛的应用。值得注意的是，当p=2时（即最小的质数），费马小定理仍然成立，尽管在这种情况下定理的表述变得非常简单（因为任何整数a模2的余数只能是0或1）。

欧拉函数：欧拉函数φ(n)是一个重要的数论函数，它表示小于或等于n的正整数中与n互质的数的个数。对于质数p来说，φ(p)=p-1。因此，对于最小的质数2来说，φ(2)=1（即1是与2互质的唯一正整数）。

结语

综上所述，2作为最小的质数，在数学世界中扮演着举足轻重的角色。它不仅在理论上为我们揭示了质数的本质和特性，还在实际应用中为我们提供了宝贵的工具和资源。从计算机科学到密码学，从几何学到物理化学，2的身影无处不在。它像一颗璀璨的明珠，照亮了我们探索数学奥秘的道路。

在未来的数学研究中，我们期待能够发现更多关于2的奥秘和特性。或许有一天，我们会找到证明或反驳哥德巴赫猜想的方法；或许有一天，我们会发现2在更高维度的空间结构中有着更加复杂的表现形式。但无论未来如何发展，2作为最小的质数这一事实将永远铭刻在数学的历史长河中，成为我们不断前行的动力源泉。