揭秘：分式背后的数学奥秘究竟是什么？

揭秘分式：解锁数学世界的神奇密码

在数学这个浩瀚而神秘的领域中，有无数的概念、公式和定理等待着我们去探索和理解。其中，“分式”这个看似简单却内涵丰富的数学概念，就像一把钥匙，能够打开通往更复杂、更深刻数学世界的大门。那么，分式究竟是什么？它有哪些特性和应用？又如何在数学和日常生活中扮演着重要的角色呢？让我们一起揭开分式的神秘面纱，解锁数学世界的神奇密码。

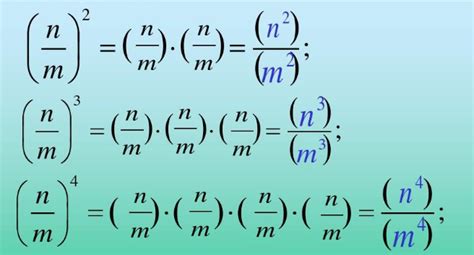
一、分式的定义与基本结构

首先，我们需要明确分式的定义。分式，顾名思义，就是分数的另一种表现形式，通常用来表示两个整数的除法运算结果。一个标准的分式由一个分子和一个分母组成，它们之间用一条横线分隔。例如，在分式a/b中，a是分子，b是分母，而这条横线则代表除法运算。

分式的基本结构虽然简单，但它所蕴含的数学思想却极为深刻。分子和分母可以代表任何实数，甚至是变量或复杂的表达式。这种灵活性使得分式在解决各种数学问题时都显得游刃有余。

二、分式的性质与运算

分式具有许多独特的性质，这些性质是理解和运用分式的基础。

1. 分式的基本性质

等价性：如果两个分式的分子和分母分别相等（或可以化简为相等），则这两个分式等价。

互逆性：一个分式与其倒数相乘，结果为1（当分母不为0时）。

约分与通分：通过约分，我们可以将分式化简为最简形式；而通过通分，我们可以将几个分式转化为具有相同分母的形式，便于进行加减运算。

2. 分式的运算

加法与减法：在进行分式的加减运算时，我们首先需要找到这些分式的最小公倍数作为通分母，然后将它们的分子进行加减运算。

乘法与除法：分式的乘法运算相对简单，只需将分子与分子相乘、分母与分母相乘即可。而分式的除法运算则可以转化为乘法运算，即“除以一个数等于乘以这个数的倒数”。

三、分式的应用与实例

分式不仅在数学理论中占据重要地位，还在实际应用中发挥着重要作用。

1. 解决实际问题

比例问题：分式在表示比例关系时非常直观和方便。例如，我们可以用分式来表示某地区男性和女性的比例、某商品的销售额与成本的比例等。

速度、时间和距离问题：在物理学和日常生活中，我们经常需要用到速度、时间和距离之间的关系。而分式正是表示这种关系的有力工具。例如，速度可以表示为距离与时间的比值（v=s/t）。

2. 数学领域的应用

方程与不等式：分式方程和不等式是数学中的常见问题。通过运用分式的性质和运算规则，我们可以求解这些方程和不等式。

函数与图像：分式函数在函数论中占有重要地位。它们的图像通常具有一些特殊的性质，如渐近线、对称性等。通过研究这些性质，我们可以更深入地理解分式函数的本质。

四、分式的深入学习与实践

对于想要深入学习和掌握分式的同学来说，以下是一些建议和实践方法。

1. 基础知识的巩固

熟记分式的性质和运算规则：这是学习分式的基础。只有熟练掌握了这些基础知识，才能进行更深入的学习和实践。

多做练习题：通过大量的练习题来巩固所学知识，提高解题能力和速度。

2. 拓展学习的路径

学习分式方程与不等式的解法：这是提高数学水平的重要一步。通过解决这些问题，我们可以锻炼自己的逻辑思维能力和数学素养。

研究分式函数的性质与图像：这有助于我们更全面地理解分式函数的本质和应用。

3. 实践应用的探索

将分式应用于实际问题：尝试用分式来解决日常生活中的问题，如计算比例、速度等。这不仅可以提高我们的数学应用能力，还可以增强我们的学习兴趣和动力。

参与数学竞赛或研究项目：通过参与这些活动，我们可以与更多的数学爱好者交流和学习，共同探索数学世界的奥秘。

五、结语

分式作为数学中的一个基本概念，具有广泛的应用价值和深刻的数学意义。通过学习和掌握分式的性质和运算规则，我们可以解决各种实际问题，提高自己的数学素养和逻辑思维能力。同时，分式也是我们通向更复杂、更深刻数学世界的一把钥匙。它引导我们不断探索、不断发现数学中的新知识和新规律。

在这个过程中，我们可能会遇到各种困难和挑战，但只要我们坚持不懈地努力学习和实践，就一定能够掌握分式的精髓，并在数学学习的道路上不断前行。让我们一起揭开分式的神秘面纱，用智慧和勇气去探索数学世界的无限可能！