揭秘：平行四边形面积的轻松计算方法

平行四边形的面积计算是几何学中的一个基础而重要的知识点。无论是在日常生活中解决实际问题，还是在学术研究中进行图形分析，掌握这一计算方法都显得尤为关键。本文将详细介绍平行四边形的面积计算公式及其推导过程，同时提供一些实用技巧和实例，帮助读者更好地理解和应用这一知识。

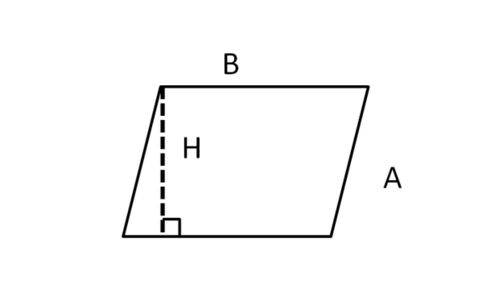
首先，我们需要明确平行四边形的定义。平行四边形是一个四边形，其中两组对边分别平行。这个性质使得平行四边形具有独特的几何特征，也是其面积计算公式的基础。

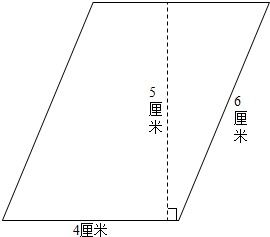
平行四边形的面积计算公式是：面积 = 底 × 高。其中，“底”是指平行四边形任意一条边，“高”则是从这条边到其平行对边的垂直距离。这个公式的推导依赖于平行四边形的性质以及直角三角形的面积计算公式。

为了更直观地理解这一公式，我们可以采用图形转化的方法。假设我们有一个平行四边形ABCD，其中AB和CD为一对平行边，BC和AD为另一对平行边。我们可以沿着平行四边形的一条对角线（例如AC）将其分割成两个三角形，即△ABC和△CDA。由于平行四边形的对角线互相平分，所以这两个三角形在底和高上都是相等的。

接下来，我们观察其中一个三角形，例如△ABC。这个三角形的底可以是AB，高就是从A到BC的垂直距离，也就是平行四边形的高。根据直角三角形的面积计算公式（面积 = 1/2 × 底 × 高），我们可以得出△ABC的面积。由于△CDA与△ABC全等，所以它们的面积也是相等的。

因此，平行四边形ABCD的面积就是这两个三角形面积的和。由于两个三角形的面积相等，所以平行四边形ABCD的面积就是其中一个三角形面积的两倍，即底AB乘以高再乘以1/2的两倍，简化后就得到了平行四边形的面积公式：面积 = 底 × 高。

需要注意的是，在计算平行四边形面积时，底和高的选择并不是唯一的。我们可以选择平行四边形任意一条边作为底，然后找到从这条边到其平行对边的垂直距离作为高。不同的底和高组合可能会得到相同的面积结果，这是因为平行四边形的面积是由其形状和大小决定的，而不是由底和高的具体位置决定的。

在实际应用中，计算平行四边形面积时常常需要借助一些工具或技巧。例如，当平行四边形的底和高不是直接给出时，我们可以通过测量或计算来得到它们。有时候，我们还需要利用平行四边形的其他性质（如对角线互相平分、内角和为360度等）来辅助计算。

此外，对于一些特殊的平行四边形（如矩形、菱形等），它们的面积计算公式可以进一步简化。例如，矩形的面积就是其长和宽的乘积；菱形的面积则是其对角线乘积的一半（需要利用勾股定理来计算对角线长度）。这些特殊平行四边形的面积计算公式虽然看起来与一般的平行四边形面积公式不同，但实际上都是基于平行四边形面积公式推导出来的。

下面，我们通过一些实例来进一步说明平行四边形面积的计算方法。

实例一：计算一个底为8厘米、高为5厘米的平行四边形的面积。

根据平行四边形的面积公式：面积 = 底 × 高，我们可以直接将给定的底和高代入公式进行计算。所以，这个平行四边形的面积就是8厘米 × 5厘米 = 40平方厘米。

实例二：计算一个对角线长度为10厘米和6厘米、且其中一个内角为60度的菱形的面积。

由于菱形是特殊的平行四边形（四边等长），我们可以通过计算其对角线长度来得到其面积。根据菱形面积的计算公式：面积 = 对角线1 × 对角线2 ÷ 2，我们需要先求出菱形的另一条对角线长度。由于菱形的一个内角为60度，且对角线互相垂直平分，所以我们可以利用30-60-90度直角三角形的性质来求出另一条对角线的长度（需要用到三角函数或特殊三角形的性质）。但在这里，为了简化计算，我们可以直接利用给定的对角线长度和菱形面积公式进行计算：面积 = 10厘米 × 6厘米 ÷ 2 = 30平方厘米。需要注意的是，这里我们并没有真正求出另一条对角线的具体长度，而是直接利用了菱形面积公式进行了计算。

通过以上两个实例，我们可以看出平行四边形面积计算在实际应用中的灵活性和实用性。无论是对于简单的平行四边形还是复杂的特殊平行四边形（如矩形、菱形等），我们都可以通过适当的方法和技巧来求出其面积。

总之，平行四边形的面积计算是几何学中的一个重要知识点。掌握这一计算方法不仅有助于我们解决日常生活中的实际问题，还能提高我们的几何思维能力和空间想象能力。希望本文的介绍能够帮助读者更好地理解和应用平行四边形面积的计算方法，并在实际学习和工作中发挥更大的作用。