掌握顶点式配方技巧,轻松求解二次函数
作者:佚名 来源:未知 时间:2024-11-27
在数学领域中,二次函数是一个重要的概念,广泛应用于物理、工程、经济等多个学科。二次函数的图像是一个抛物线,而抛物线的形状、位置和方向由它的顶点决定。因此,掌握二次函数的顶点式及其配方方法,对于理解和应用二次函数至关重要。
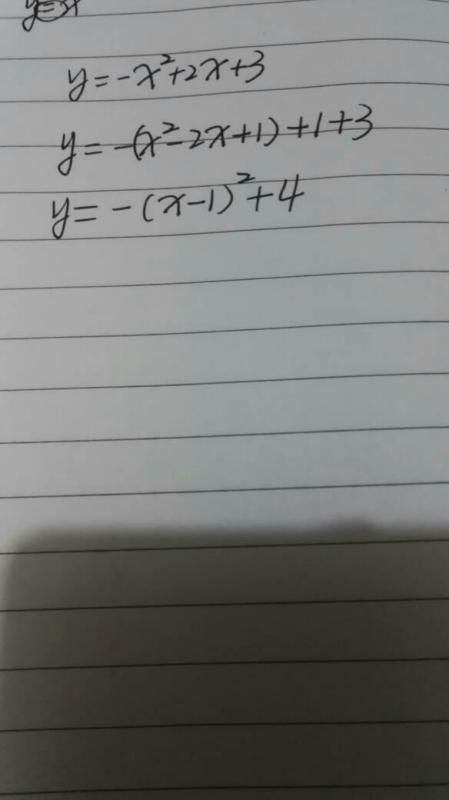
一、顶点式的定义与形式
顶点式是二次函数的一种表示形式,它直接给出了抛物线的顶点坐标和开口方向。顶点式的一般形式为:
y = a(x - h)^2 + k
其中,(h, k)是抛物线的顶点坐标,a是二次项系数,决定了抛物线的开口方向和宽度。当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。
二、配方过程详解
配方是将一般形式的二次函数转化为顶点式的过程。一般形式的二次函数为:
y = ax^2 + bx + c
要将它转化为顶点式,需要完成以下步骤:
1. 提取二次项系数:
首先,将二次项系数a提取出来,得到:
y = a(x^2 + (b/a)x) + c
2. 配方:
接下来,对括号内的部分进行配方。配方的目的是将x^2 + (b/a)x转化为完全平方的形式。为此,我们需要加上和减去(b/(2a))^2,即:
y = a(x^2 + (b/a)x + (b/(2a))^2 - (b/(2a))^2) + c
3. 整理:
将上式进一步整理,得到:
y = a((x + b/(2a))^2 - (b^2)/(4a^2)) + c
= a(x + b/(2a))^2 - (ab^2)/(4a^3) + c
= a(x + b/(2a))^2 + (4ac - b^2)/(4a)
= a(x - (-b/(2a)))^2 + (4ac - b^2)/(4a)
此时,我们已经成功地将一般形式的二次函数转化为顶点式,其中顶点坐标为(-b/(2a), (4ac - b^2)/(4a))。
三、配方的几何意义
配方不仅是一个代数过程,它还具有深刻的几何意义。在几何上,配方相当于对抛物线进行平移变换,使其顶点位于原点或指定的位置。
1. 平移变换:
对于一般形式的二次函数y = ax^2 + bx + c,我们可以通过配方将其转化为顶点式y = a(x - h)^2 + k。这个转化过程实际上是对抛物线进行了平移变换:先沿x轴平移-b/(2a)个单位,再沿y轴平移(4ac - b^2)/(4a)个单位。
2. 顶点坐标的求解:
通过配方,我们可以直接读出抛物线的顶点坐标(h, k),其中h = -b/(2a),k = (4ac - b^2)/(4a)。这两个坐标值对于确定抛物线的位置和形状至关重要。
四、配方的应用实例
配方在解决二次函数问题时具有广泛的应用。以下是一些典型的应用实例:
1. 求抛物线的顶点坐标:
给定二次函数的一般形式y = ax^2 + bx + c,我们可以通过配方求出其顶点坐标(h, k),其中h = -b/(2a),k = (4ac - b^2)/(4a)。
例如,对于函数y = 2x^2 - 4x + 1,我们可以将其转化为顶点式y = 2(x - 1)^2 - 1,从而直接读出顶点坐标为(1, -1)。
2. 求抛物线的最大值或最小值:
对于开口向上的抛物线(a > 0),其顶点坐标对应的y值为最小值;对于开口向下的抛物线(a < 0),其顶点坐标对应的y值为最大值。通过配方求出顶点坐标后,我们可以直接得出抛物线的最大值或最小值。
例如,对于函数y = -3x^2 + 6x - 1,我们可以将其转化为顶点式y = -3(x - 1)^2 + 2,从而得出该函数的最大值为2。
3. 抛物线的对称性质:
抛物线是关于其对称轴对称的。对于顶点式为y = a(x - h)^2 + k的抛物线,其对称轴为直线x = h。通过配方求出顶点坐标后,我们可以直接得出抛物线的对称轴。
例如,对于函数y = (x + 2)^2 - 4,我们可以直接读出其对称轴为直线x = -2。
4. 抛物线的开口方向和宽度:
通过配方求出的二次项系数a决定了抛物线的开口方向和宽度。当a > 0时,抛物线开口向上;当a < 0时,抛物线开口向下。而抛物线的宽度则与|a|的倒数成正比,即|a|越大,抛物线越窄;|a|越小,抛物线越宽。
五、配方的注意事项
在进行配方时,需要注意以下几点:
1. 保持等式平衡:
在配方过程中,需要确保等式两边始终保持平衡。每当我们对等式的一边进行变换时,都需要对另一边进行相应的变换。
2. 注意符号变化:
在配方过程中,需要注意符号的变化。特别是当我们将二次项系数提取出来后,需要确保括号内的部分保持正确的符号。
3. 检查计算结果:
配方完成后,需要检查计算结果是否正确。可以通过将顶点式展开成一般形式,并与原函数进行比较来验证结果的正确性。
六、结语
配方是二次函数学习中的一个重要环节,它不仅能够将一般形式的二次函数转化为顶点式,从而方便地求出抛物线的顶点坐标、最大值或最小值、对称轴等关键信息;而且能够加深对二次函数性质的理解和应用能力。因此,在学习二次函数时,我们应该熟练掌握配方的方法和技巧,并能够灵活运用它们来解决实际问题。
- 上一篇: 轻松学会!幼儿园级简笔画月亮绘制教程
- 下一篇: 如何快速找到周边的医院











































