揭秘勾股定理的绝妙证明方法

勾股定理，又称毕达哥拉斯定理，是数学中一条极为重要的定理。它表明在一个直角三角形中，直角边的平方和等于斜边的平方。具体公式为：a² + b² = c²，其中a和b为直角三角形的两条直角边，c为斜边。这个定理不仅在数学领域有着广泛的应用，而且在物理学、工程学等多个领域也发挥着重要作用。那么，如何证明勾股定理呢？本文将介绍几种经典的证明方法，让读者领略这一古老定理的奇妙与魅力。

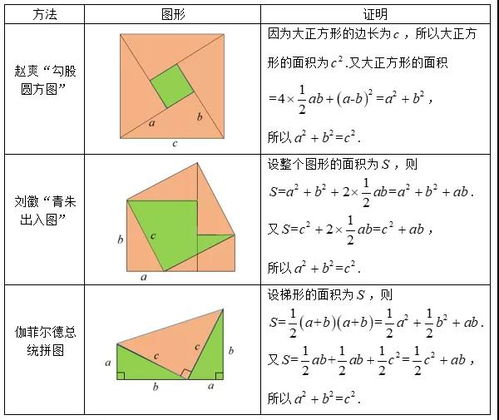
方法一：面积法证明

这是勾股定理的一种直观且易于理解的证明方法。

步骤一：图形构建

首先，画一个直角三角形ABC，其中∠C为直角，AC和BC为直角边，AB为斜边。接着，以AC和BC为边分别向外作两个正方形ACDE和BCFG，再以AB为边向外作正方形ABHI。

步骤二：面积计算

然后，观察图形可以发现，正方形ABHI的面积等于两个正方形ACDE和BCFG的面积之和减去四个直角三角形的面积。具体计算如下：

正方形ABHI的面积 = AB²

正方形ACDE的面积 + 正方形BCFG的面积 = AC² + BC²

四个直角三角形的面积（以AC、BC为直角边）总和为2个三角形ABC的面积，即2×(1/2)×AC×BC = AC×BC

步骤三：等式推导

根据面积相等原则，可以列出等式：

AB² = AC² + BC² - 2×(1/2)×AC×BC + 2×(1/2)×AC×(BC边上的高) + 2×(1/2)×BC×(AC边上的高)

由于三角形ABC的面积也可以表示为1/2×AB×斜边上的高，而斜边上的高在直角三角形中实际上等于另一条直角边（由直角三角形的面积公式可知），因此上式中的高可以相互抵消，最终简化为：

AB² = AC² + BC²

从而证明了勾股定理。

方法二：相似三角形证明

这种方法利用了相似三角形的性质来推导勾股定理。

步骤一：图形构建

同样，画一个直角三角形ABC，其中∠C为直角。过直角顶点C作斜边AB上的高CD，交AB于点D。

步骤二：相似三角形识别

观察图形，可以发现直角三角形ADC与直角三角形ACB相似，直角三角形CDB与直角三角形ACB也相似。

步骤三：比例关系推导

根据相似三角形的性质，有：

AC/AB = CD/BC

BC/AB = CD/AC

将两式交叉相乘，得到：

AC×BC = AB×CD

同时，由于三角形ABC的面积也可以表示为1/2×AC×BC（以AC、BC为底），以及1/2×AB×CD（以AB为底，CD为高），因此上式实际上表示了两种计算三角形面积的方法相等。

步骤四：勾股定理推导

对AC²和BC²进行拆分和组合，利用平方差公式和上述面积相等关系，可以推导出：

AC² = AD² + CD²（由勾股定理在直角三角形ADC中得出）

BC² = BD² + CD²（由勾股定理在直角三角形CDB中得出）

将两式相加，得到：

AC² + BC² = AD² + BD² + 2×CD²

由于AD + BD = AB，所以上式可以进一步化简为：

AC² + BC² = AB²

从而证明了勾股定理。

方法三：总统证法（欧几里得证法）

这种方法是古希腊数学家欧几里得在《几何原本》中给出的证明，具有极高的历史价值。

步骤一：图形构建

画一个直角三角形ABC，其中∠C为直角。过直角顶点C作两条射线CE和CF，分别垂直于AB的延长线和反向延长线，交于点E和F。

步骤二：平行线构造

过点A作AD∥CF交EF于点D，再过点B作BG∥CE交EF于点G。

步骤三：相似三角形与平行四边形识别

观察图形，可以发现四边形ADGB是平行四边形（由AD∥BG和AB∥DG得出），且∠A=∠GCE，∠B=∠GCF（由平行线的交替内角性质得出）。

因此，三角形ADC与三角形GCE相似，三角形BDF与三角形GCF相似。

步骤四：比例关系与面积计算

根据相似三角形的性质，有：

AC/CE = AD/CG

BC/CF = BD/CG

由于ADGB是平行四边形，所以AD=BG，BD=AG。

将两式相加，得到：

AC/CE + BC/CF = (AD+BD)/CG = AB/CG

同时，由于三角形ABC的面积等于平行四边形ADGB面积的一半（因为它们有相同的底和高的一半），而平行四边形ADGB的面积等于矩形CEGF的面积（因为它们有相同的对边），所以三角形ABC的面积也可以表示为1/2×CE×CF。

步骤五：勾股定理推导

利用上述面积相等关系，结合平方差公式和比例关系，可以推导出：

AC² = AE×AB（由三角形ADC与三角形ABE相似得出）

BC² = BF×AB（由三角形BDF与三角形BFA相似得出）

将两式相加，并利用AE+BF=EF-2×(CE或CF的某个部分，这部分在推导中可以相互抵消)，最终可以得到：

AC² + BC² = AB²

从而证明了勾股定理。

结语

勾股定理的证明方法多种多样，每一种方法都蕴含着数学的智慧和魅力。通过本文的介绍，读者可以了解到面积法、相似三角形法和总统证法这三种经典的证明方法。这些证明方法不仅展示了数学的严谨性和逻辑性，也让我们更加深刻地理解了勾股定理的本质和应用。希望读者在阅读本文后，能够对勾股定理有更深入的认识和理解。