掌握史丰收速算法：轻松学会一位数加法指算技巧

史丰收速算法——指算加法之一位数加法

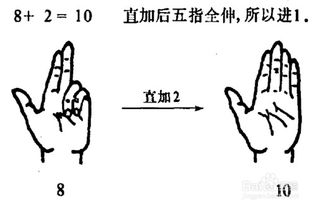
史丰收速算法，是由国际著名发明家史丰收教授首创的一套少儿智能开发体系。该算法通过左手五个手指的伸屈结合大脑的记忆进行运算，极大地提高了计算速度，减少了思维负担。联合国教科文组织誉之为教育科学史上的奇迹，并向全球少年儿童推荐这一开发智能的金钥匙。本文将详细介绍史丰收速算法中的指算加法之一位数加法，帮助读者全面理解这一独特的计算方法。

一、史丰收速算法的背景

史丰收教授1956年出生于中国陕西省大荔县，自幼对数学有着浓厚的兴趣。从11岁开始，他用了十年的时间钻研速算法，终于成功创立了一套不用计算工具、不列运算程序、从高位算起的快速计算法。1978年，史丰收速算法通过了中科院、计算所、数学所和应用数学推广办公室的考核鉴定，从此公布于世。这一创新成果不仅在国内受到高度评价，还引起了国际学术界的广泛关注。

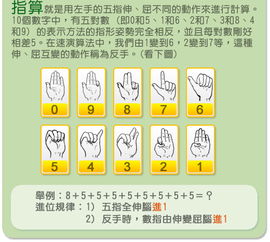
二、史丰收速算法的特点

史丰收速算法的主要特点包括以下几点：

1. 从高位算起：传统的计算方法是从低位算起，而史丰收速算法则是从高位算起，使得读、写、算数的顺序一致，大大提高了计算速度。

2. 脑口手并用：速算法结合了大脑的记忆、口头的表达和手指的动作，三者协同工作，使得计算过程更加高效。

3. 口诀与规律：史丰收速算法总结了一系列计算口诀和规律，通过学习和掌握这些口诀，能够快速进行加、减、乘、除等运算。

4. 适用性广：史丰收速算法不仅可以用于加减乘除的基本运算，还可以应用于乘方、开方、三角函数、对数等高级数学运算。

三、指算加法之一位数加法

史丰收速算法中的指算加法之一位数加法，是通过左手五个手指的伸屈来进行数字运算的。以下详细介绍这一方法的几个关键概念和具体步骤。

1. 关键概念

内凑：两数之和等于5时，便说这两数互为内凑。如2和3、1和4、5和0。

外凑：大于5而小于10的数中，超过5的部分叫做该数的外凑。如1是6的外凑（6=5+1），2是7的外凑（7=5+2）。

补数：两数之和等于10、100、1000……时，便说他们对于10、100、1000……互为补数。互补的两数的有效末位之和是10，其余各位之和都是9。

反手：任何相差5的两个指型都是伸屈相反，加5时一定是将原来弯曲的手指伸开并把原来伸开的手指弯曲起来，这种动作叫反手。即“加5反手”。

2. 具体步骤

史丰收速算法中的指算加法之一位数加法，根据加数的大小和具体情况，可以分为以下几种情况：

直加：当加数不大于被加数的虚指时，直接改变虚指的姿势，屈的虚指改为伸的，伸的改为屈的。注意：这时的加数不能大于5，因为虚指数不能多于5个。

示例：6+3=9

过程：六的指型为大拇指、食指、中指伸直，无名指和小指弯曲。加3时，由于3不大于5，可以直接将无名指和小指伸直，得到9的指型（大拇指、食指、中指、无名指伸直，小指弯曲）。

反手加：当加数小于5而虚指不够用时，把加数改为“5-内凑”，即指算的动作变为先反手，再从反手后的数指里减内凑，也可以先从被加数的数指里减内凑再反手。

示例：4+3=7

过程：四的指型为大拇指、食指、中指、无名指弯曲，小指伸直。加3时，由于3小于5但虚指不够用，先将小指弯曲（反手），得到五的指型（大拇指、食指、中指、无名指、小指均弯曲），再从五指中减去内凑2（因为3的内凑是2），得到七的指型（大拇指、食指、中指伸直，无名指、小指弯曲）。

加外凑：当加数大于5时，加数等于5加它的外凑，这时加法应分成两步，首先是反手，再就是加外凑。

示例：8+8=16

过程：八的指型为大拇指、食指、中指、无名指伸直，小指弯曲。加8时，由于8大于5，先将小指弯曲（反手），得到五的指型，再加外凑3（因为8的外凑是3），由于此时虚指不够用，需要进位。在脑海中记住进位1，再从数指中减去补数2（因为8的补数是2），最终得到16的指型（此时由于进位，实际上是在脑海中计算得到结果）。

四、练习与应用

为了熟练掌握史丰收速算法中的指算加法之一位数加法，读者可以通过大量的练习来加深理解和记忆。以下是一些练习题目：

1. 直加练习：0+1、1+1、2+2、3+3、4+1、5+0

2. 反手加练习：4+2、9+2、3+4、8+3

3. 加外凑练习：6+6、7+7、8+8、9+9

通过反复练习，读者可以逐渐掌握这一方法的技巧，提高计算速度和准确性。同时，也可以将这一方法应用到实际生活中，解决各种需要快速计算的场景。

五、结语

史丰收速算法是一种高效、快捷的计算方法，指算加法之一位数加法则是其中的基础部分。通过学习和掌握这一方法，读者可以大大提高自己的计算能力，同时也有助于开发智力和提高思维、分析、判断的能力。希望本文能够帮助读者全面了解史丰收速算法，并在实际学习和生活中加以应用。