Excel中计算两组数据相关性的方法
作者:佚名 来源:未知 时间:2024-12-21
在Excel中计算两组数据的相关性,是数据分析中非常实用的一项技能。无论你是在学术研究、商业分析,还是日常生活中的数据整理,掌握这一技能都能帮助你更好地理解数据之间的关系,从而做出更明智的决策。接下来,我们将详细介绍在Excel中如何计算两组数据的相关性,包括使用散点图、计算皮尔逊相关系数以及执行回归分析等方法。
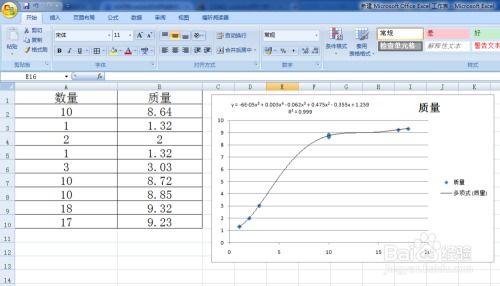
使用散点图直观查看数据关系
散点图是Excel中一种非常直观的数据可视化工具,通过绘制散点图,你可以快速观察数据点的分布模式,从而判断两个变量之间是否存在某种关系。以下是使用散点图的步骤:
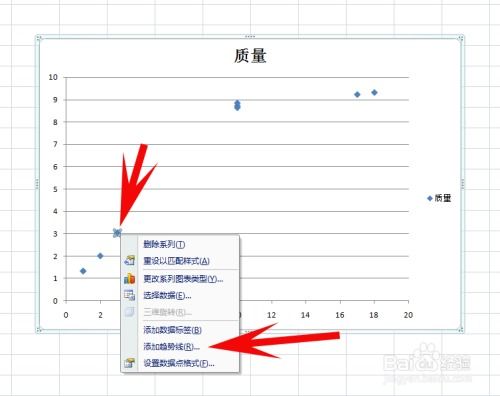
1. 选择数据:在Excel中,选择你想要分析的两组数据。通常,这两组数据会放在两个相邻的列中。
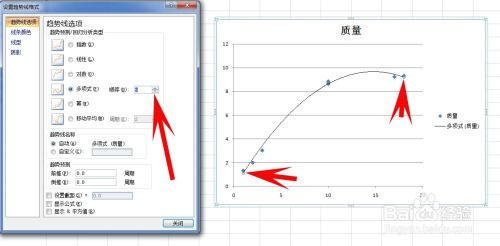
2. 插入散点图:在Excel顶部菜单中,点击“插入”选项卡,然后选择“散点图”。在散点图下拉菜单中,选择你想要的图表类型,通常会选择第一个选项“带直线的散点图”。
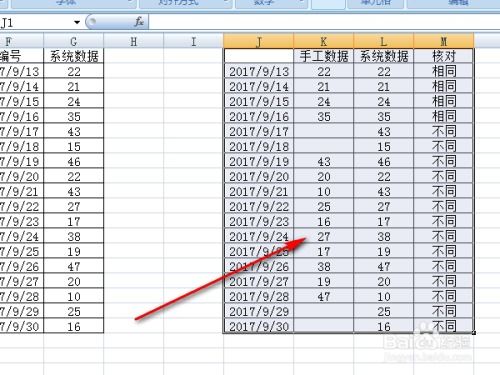
3. 调整图表:图表生成后,你可以对其进行调整,比如添加标题、轴标签、网格线等。点击图表中的任何元素(如标题或轴标签),然后输入你想要显示的文本。
通过观察散点图,你可以看到数据点是否有某种模式或趋势。例如,如果数据点大致沿着一条直线排列,则表明两组数据之间可能存在线性关系;如果数据点分布较为随机,则表明两组数据之间可能没有明显的相关性。
计算皮尔逊相关系数
皮尔逊相关系数是衡量两个变量之间线性关系强度和方向的一个重要指标,通过计算皮尔逊相关系数,你可以量化两组数据之间的相关性。皮尔逊相关系数的取值范围在-1到1之间,其中1表示完全正相关,-1表示完全负相关,0表示没有相关性。
以下是计算皮尔逊相关系数的步骤:
1. 选择数据:确保你的数据按列排列,选择你要分析的两组数据。
2. 使用公式:在一个空白单元格中输入公式`=CORREL(array1, array2)`,其中`array1`和`array2`分别是你的两组数据的范围。例如,如果你的数据在A列和B列,从第1行到第10行,那么公式应为`=CORREL(A1:A10, B1:B10)`。
3. 解释结果:公式返回一个介于-1和1之间的数值。如果相关系数接近1,则表示两组数据高度正相关;如果接近-1,则表示高度负相关;如果接近0,则表示没有显著的线性相关性。
皮尔逊相关系数不仅可以帮助你判断数据之间的关系方向(正相关或负相关),还可以量化这种关系的强度。例如,如果你计算得出的皮尔逊相关系数为0.85,这表示两组数据之间有强烈的正相关性。反之,如果相关系数为-0.85,则表示两组数据有强烈的负相关性。这个数值不仅帮助你理解数据的关系,还可以作为后续分析和决策的重要依据。
执行回归分析
回归分析是一种统计方法,用于确定一个或多个自变量对因变量的影响。通过回归分析,你不仅可以了解两组数据之间的线性关系,还可以建立一个预测模型,用来预测因变量的未来值。以下是执行回归分析的步骤:
1. 选择数据:在Excel中,选择你要分析的两组数据,通常会将自变量放在X轴,因变量放在Y轴。
2. 插入回归图表:在Excel顶部菜单中,点击“数据”选项卡,然后选择“数据分析”。在弹出的对话框中,选择“回归”选项,然后点击“确定”。
3. 设置参数:在回归分析对话框中,输入自变量和因变量的数据范围。例如,如果自变量在A列,因变量在B列,从第1行到第10行,那么输入范围应为A1:A10和B1:B10。
4. 生成结果:点击“确定”后,Excel会生成一份回归分析报告,其中包含多个统计指标,如R平方值、回归系数、显著性水平等。
通过回归分析,你不仅可以了解两组数据之间的线性关系,还可以评估模型的拟合度。例如,如果R平方值较高,说明模型对数据的解释能力较强;如果回归系数显著,说明自变量对因变量有显著影响。这些信息对于商业决策、市场分析等领域非常有帮助。
注意事项
在进行相关性分析时,需要注意以下几点:
1. 数据清理:确保你的数据干净且格式正确,处理缺失值和异常值,以提高分析结果的准确性。
2. 理解相关性与因果关系:相关性并不代表因果关系。两个变量之间的相关性只是表明它们之间存在某种联系或关联,但并不一定能够说明其中一个变量的变化是导致另一个变量发生变化的原因。
3. 选择合适的分析方法:根据数据的特点和分析目的,选择合适的分析方法。例如,对于非线性关系,可以考虑使用斯皮尔曼相关系数进行分析。
案例分析
假设某家公司想要分析广告投放费用与销售额之间的关系,以便优化市场推广策略。公司收集了过去一年的广告投放费用和月度销售额数据。通过以下步骤进行分析:
1. 数据准备:对数据进行清理,处理了缺失值和异常值,并对数据进行了标准化处理。
2. 相关性分析:使用皮尔逊相关系数计算了广告投放费用与销售额之间的相关性,发现相关系数为0.85,表明两者之间有强烈的正相关性。
3. 回归分析:进行了回归分析,建立了广告投放费用与销售额之间的回归模型,发现回归系数显著,R平方值为0.72,表示模型具有较强的解释能力。
4. 策略调整:根据分析结果,公司决定增加广告投放费用,并优化广告投放渠道,以期望提高销售额。
通过这个案例,我们可以看到,通过数据相关性分析,公司能够更科学地制定市场推广策略,提高业务绩效。
结语
在Excel中计算两组数据的相关性是一项非常实用的技能,它可以帮助你更好地理解数据之间的关系,从而做出更明智的决策。无论是使用散点图、计算皮尔逊相关系数,还是执行回归分析,都是进行相关性分析的有效方法。希望这篇文章能够帮助你掌握这一技能,并在实际数据分析中发挥作用。
- 上一篇: 如何下载优酷网站上的视频文件
- 下一篇: 如何使用TinyPDF虚拟打印机






























