一元二次方程的四种求解方法

一元二次方程是数学中最为基础也最为重要的方程之一，它在代数、几何以及实际问题中都有广泛的应用。求解一元二次方程是每个学生必须掌握的技能。本文将详细介绍求解一元二次方程的四种主要方法：公式法、配方法、因式分解法和图像法。

首先，我们需要了解一元二次方程的一般形式：ax² + bx + c = 0，其中a、b和c是已知数，且a ≠ 0。这个方程表示一个关于x的二次多项式等于零，我们的目标是找到使这个多项式等于零的x的值。

公式法

公式法也称为韦达定理法，是求解一元二次方程最通用和最直接的方法。根据韦达定理，对于一元二次方程ax² + bx + c = 0，其解为：

x = [-b ± √(b² - 4ac)] / (2a)

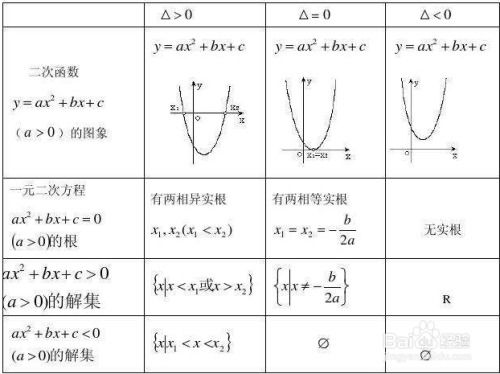
这个公式被称为一元二次方程的求根公式。其中，判别式Δ = b² - 4ac决定了方程的根的性质：

1. 当Δ > 0时，方程有两个不相等的实数根。

2. 当Δ = 0时，方程有两个相等的实数根（即一个重根）。

3. 当Δ < 0时，方程没有实数根，但有两个共轭复数根。

使用公式法求解一元二次方程的步骤：

1. 计算判别式Δ = b² - 4ac。

2. 根据判别式的值，判断方程根的情况。

3. 代入求根公式，计算方程的解。

例如，解方程3x² - 5x + 2 = 0：

1. 计算判别式Δ = (-5)² - 4×3×2 = 25 - 24 = 1。

2. 因为Δ > 0，所以方程有两个不相等的实数根。

3. 代入求根公式，得到x = [5 ± √(1)] / (2×3) = (5 ± 1) / 6，即x₁ = 1，x₂ = 2/3。

配方法

配方法是一种通过配方将一元二次方程转化为完全平方形式，从而求解的方法。配方的基本思想是将方程ax² + bx + c = 0转化为(x - h)² = k的形式，然后求解x。

使用配方法求解一元二次方程的步骤：

1. 将方程ax² + bx + c = 0移项，得到ax² + bx = -c。

2. 将二次项系数化为1，得到x² + (b/a)x = -c/a。

3. 进行配方，即方程两边同时加上(b/(2a))²，得到x² + (b/a)x + (b/(2a))² = (b/(2a))² - c/a。

4. 化简，得到(x + b/(2a))² = (b² - 4ac)/(4a²)。

5. 开方，得到x + b/(2a) = ±√((b² - 4ac)/(4a²))。

6. 解得x = [-b ± √(b² - 4ac)] / (2a)。

可以看出，配方法最终得到的解与公式法相同，但配方过程更直观地展示了方程从一般形式到完全平方形式的转化。

因式分解法

因式分解法是一种通过对方程左边进行因式分解，从而求解的方法。这种方法适用于b² - 4ac ≥ 0，即方程有实数根的情况。

使用因式分解法求解一元二次方程的步骤：

1. 将方程ax² + bx + c = 0的左边进行因式分解，得到(mx + n)(px + q) = 0。

2. 根据因式分解的结果，分别令每个因式等于零，得到mx + n = 0和px + q = 0。

3. 解得x = -n/m和x = -q/p。

例如，解方程2x² - 5x + 3 = 0：

1. 将方程左边进行因式分解，得到(2x - 3)(x - 1) = 0。

2. 分别令每个因式等于零，得到2x - 3 = 0和x - 1 = 0。

3. 解得x₁ = 3/2，x₂ = 1。

因式分解法需要一定的技巧和经验，但对于一些特殊的方程，如系数为整数且容易分解的方程，因式分解法往往比公式法更快捷。

图像法

图像法是一种通过绘制函数图像，观察图像与x轴的交点，从而求解一元二次方程的方法。这种方法虽然不如前三种方法精确，但具有直观、形象的特点，有助于理解一元二次方程根的概念。

使用图像法求解一元二次方程的步骤：

1. 将方程ax² + bx + c = 0转化为函数y = ax² + bx + c。

2. 在坐标系中绘制函数y = ax² + bx + c的图像。

3. 观察图像与x轴的交点，交点对应的x值即为方程的解。

需要注意的是，图像法得到的解通常是近似的，特别是在判别式Δ接近零或方程系数较大时，图像法可能不够精确。因此，在精确求解一元二次方程时，还是推荐使用公式法、配方法或因式分解法。

综上所述，求解一元二次方程有公式法、配方法、因式分解法和图像法四种主要方法。每种方法都有其特点和适用范围，在实际应用中，我们可以根据方程的具体形式和求解需求选择合适的方法。通过熟练掌握这些方法，我们可以更加高效地求解一元二次方程，为学习和工作打下坚实的基础。